Почему динамическое светорассеяние плохо работает при высоких концентрациях?
Динамическое рассеяние света (DLS) - это эффективный метод, долгое время с успехом используемый для анализа гидродинамического размера различных наночастиц. Несмотря на универсальность этого метода, есть несколько важных соображений, которые нельзя игнорировать при анализе высококонцентрированных коллоидов. Многие производители указывают на возможность использования их DLS приборов для анализа концентрированных коллоидов без разбавления. Однако, на практике такие измерения крайне трудно интерпретировать. Почему это так? Прежде всего, анализ концентрированных коллоидов ставит дополнительные вопросы относительно самого понятия «гидродинамический размер». Чтобы разобраться в причинах, нам нужно обсудить два эффекта, встречающихся в концентрированных растворах: многократное светорассеяние и совместная диффузия.
Динамическое светорассеяние измеряет параметры диффузии частиц и, на основании этих данных, высчитывает гидродинамический размер. Все свободно диффундирующие частицы подвергаются броуновскому движению, которое пропорционально тепловой энергии, выраженной как произведение постоянной Больцмана на температуру (kbT). Отдельная частица будет диффундировать со скоростью обратно пропорциональной ее размеру, поэтому коэффициент диффузии DT этой частицы можно использовать для расчета ее гидродинамического диаметра, dH, как показано в уравнении Стокса-Эйнштейна:
DT = kb T / 3πηdH
dH может быть рассчитан, если известны температура и вязкость вмещающей среды η. Коэффициент диффузии отдельной частицы является результатом «индивидуальной диффузии»; в пределе бесконечного разбавления рассчитанный размер полностью эквивалентен гидродинамическому размеру. В простейшем случае, единичная скорость затухания Г извлекается из автокорреляционной функции DLS (АКФ). Г является обратной величиной характерного времени релаксации τt, что математически может быть выражено как:
g (1) (τ) = exp (-G τ)
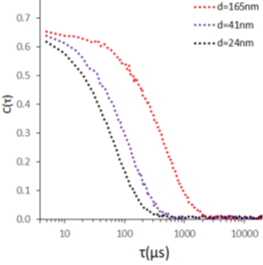
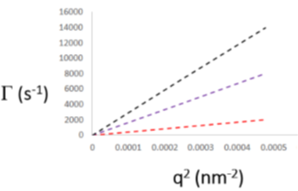
Рис. 1.0 Моделированные АКФ для скоростей затухания Г = 7000, 4000 и 1000 с-1 (соответствующих сферическим частицам диаметром 24, 41 и 165 нм). Связь между Г и гидродинамическим размером будет рассмотрена в следующих разделах.
Обратите внимание, что большая скорость затухания соответствует наименьшему эффективному размеру частиц, который в пределе бесконечного разбавления соответствует коэффициенту диффузии отдельной частицы. Коэффициент диффузии может быть получен из наклона приведенного выше графика. При анализе подавляющего большинства компактных глобулярных частиц, для получения их гидродинамического размера можно использовать один угол светорассеяния.
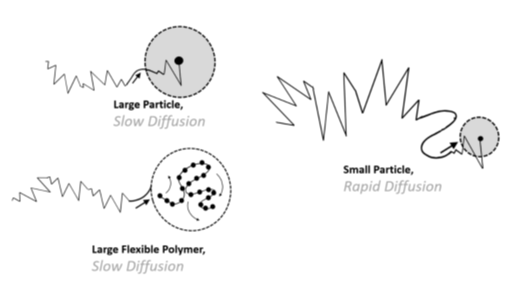
Рис. 1.1 Показаны две сферические частицы, большая частица будет диффундировать медленнее. Также следует отметить, что гибкие полимеры часто имеют несколько режимов релаксации, соответствующих диффузии, а также внутреннему движению полимерной цепи.
Скорость диффузии частиц непосредственно пересчитывается в гидродинамический размер, где быстрые скорости затухания соответствуют более мелким частицам, а более низкие скорости затухания соответствуют более крупным частицам. Для данного значения q Г связано с коэффициентом трансляционной диффузии DT по следующему уравнению:
DT = Г / q2
Для такого расчета все флуктуации автокорреляционной функции рассматриваются как результат диффузии, а все коэффициенты диффузии рассматриваются как результаты теплового движения индивидуальных частиц. К сожалению, это всего лишь математическая аппроксимация. В случае с реальными образцами все обстоит гораздо сложнее. Ситуация еще больше осложняется, когда приходится учитывать взаимодействия частиц друг с другом.
Индивидуальная диффузия и совместная диффузия
Концепция бесконечного разбавления - это абстракция. Однако, делая серийные разведения концентрированного образца, Вы постепенно снижаете интенсивность взаимодействия между частицами. Благодаря уменьшению этих взаимодействий эффект совместной диффузии сводится к минимуму, и, таким образом, результирующий коэффициент диффузии приближается к значению, ожидаемому для индивидуальной диффузии. При высоких концентрациях измеренный коэффициент диффузии не будет результатом индивидуальной диффузии; таким образом, хотя он может быть измерен, вычисленный на его основании размер не будет «истинным» размером частиц. При этом, нет прямой зависимости по отношению к концентрации. В зависимости от типа взаимодействий между частицами, значения коэффициента совместной диффузии будут разными, смещая получаемые размеры частиц в меньшую или большую сторону.
Многократное светорассеяние
Если концентрация образца достаточно высока, один фотон лазерного света будет рассеиваться несколькими частицами последовательно, прежде чем достигнет детектора. Чем больше длина пути фотона, тем больше вторичных событий рассеяния происходит и тем меньше коррелирует обнаруженный свет с исходным сигналом. В отличие от условий разбавленного раствора, эта быстрая потеря корреляции не является результатом движения частиц и, следовательно, не связана с размером частиц. Смотрите рисунок 1.2.
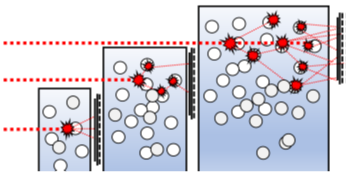
Рис. 1.2. Многократное рассеяние становится более выраженным при увеличении длины пути.
Таким образом, в случае многократного рассеяния сигнал изменяется быстрее (функция автокорреляции имеет больший наклон, падает быстрее). Программное обеспечение будет воспринимать столь быстрое изменение сигнала как результат быстрой диффузии частиц. На самом деле это изменение не связано с диффузией. Таким образом, не только вычисленный размер не является правильным размером частиц, но и сам «коэффициент диффузии», из которого рассчитывается гидродинамический размер частиц, не является реальным коэффициентом диффузии. Образцы, показывающие многократное рассеяние, будут отклоняться в сторону меньших размеров, поскольку dH ∝ kb T / DT. Степень этого перекоса будет сильно зависеть от концентрации, так что видимый размер будет систематически уменьшаться с увеличением концентрации. Однако, данное изменение не является пропорциональным и сильно зависит от свойств всех компонентов образца.
Взаимодействие частиц между собой
Одним из вариантов уменьшения влияния фактора многократного светорассеяния является минимизация «активной» длины пути, т.е. количества образца на пути луча. Однако устранение многократного рассеяния с использованием меньшей длины пути решает одну проблему, но не другие. Так, несмотря на то, что становится возможным проводить измерения при высоких концентрациях без значимого влияния эффекта многократного светорассеяния, это не устраняет эффект взаимодействия частиц друг с другом.
Итак, мы устранили артефакт множественного светорассеяния, но остается еще взаимодействие между частицами, которое препятствует измерению гидродинамических размеров индивидуальных частиц. Существует множество форм взаимодействия частиц друг с другом. Вот некоторые из них: отталкивание, притяжение, кластеризация (т.е. любые иные типы сил, которые могут создавать совместное движение). Вновь, измеряемая Вами величина не является «истинным размером», хотя теперь у Вас есть возможность получить действительный коэффициент диффузии.
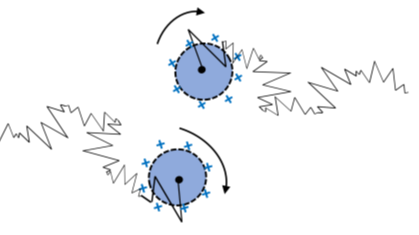
Рис. 1.3. Одним из наиболее распространённых явлений является заряд на поверхности частиц. Как показано на рисунке выше, на примере положительно заряженных коллоидных частиц, одинаковые заряды вызывают отталкивание между частицами.
При высоких концентрациях больше невозможно игнорировать потенциалы взаимодействия между частицами. Независимо от того, является ли потенциал притягивающим или отталкивающим, он все равно приводит к совместной диффузии, поскольку движения частиц больше не являются индивидуальными. Начальная зависимость между коэффициентом диффузии и концентрацией (c) может быть выражена как DT (c) = D0 (1 + kc), где k - коэффициент концентрации, связанный с силой взаимодействия. Могут встречаться члены более высокого порядка, но для получения Do (истинного коэффициента индивидуальной диффузии) и истинного размера экстраполяцию производят по линейной области c.
Истинный размер
Что значит «достаточно разбавлено»? Работа в "пределе разведения".
Последовательное разбавление - это эффективный способ определить, достаточно ли разбавлен образец для проведения адекватного измерения гидродинамических размеров с помощью DLS. По мере приближения к пределу разбавления кажущийся размер частиц стремится к предельному, или инвариантному, гидродинамическому размеру. См. ниже пример с двумя гибкими полимерами: полистиролсульфонат натрия (NaPSS) и поливинилпирролидон (PVP).
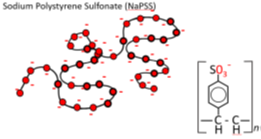
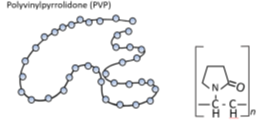
Рис. 2.0 Два сравниваемых гибких полимера - это NaPSS и PVP. NaPSS имеет высокую линейную плотность заряда, благодаря наличию постоянных отрицательных зарядов. Напротив, PVP не заряжен. Оба образца имеют одинаковую Mw и длину цепи.
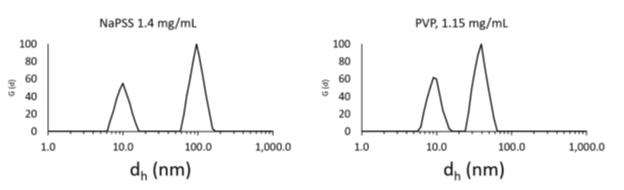
Рис. 2.1. Даже при сильном разбавлении наблюдается вторая мода в размерах с гидродинамическими размерами порядка 10 нм.
Учитывая высокую плотность заряда, частицы NaPSS очень сильно взаимодействуют друг с другом, т.к. между боковыми цепями частиц NaPSS возникает сильное электростатическое отталкивание. Графики зависимости коэффициента диффузии от концентрации для двух полимеров представлены ниже:
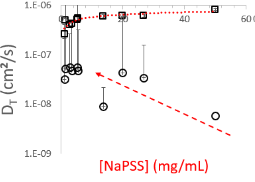
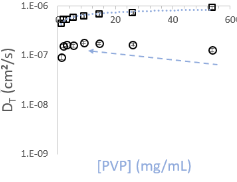
Рис. 2.2 Разведение NaPSS и PVP от исходных концентраций 50 мг/мл продолжалось до тех пор, пока измеренные коэффициенты диффузии не начали приближаться к постоянным значениям. Быстрая мода (DT> 1x10-7 см2/с), соответствуют размеру отдельной полимерной цепи.
Наибольшие концентрации для обоих коллоидных растворов составляют порядка 50 мг/мл. Оба раствора полностью оптически прозрачны, и тем не менее демонстрируют признаки многократного рассеяния и интенсивных взаимодействий между частицами. Начиная с самых высоких концентраций, оба раствора полимера демонстрируют бимодальные распределения по размерам. Коэффициент диффузии, постепенно приближается к предельному значению по мере снижения концентрации. В диапазоне концентраций 50 – 15 мг/мл, коэффициент диффузии падает очень быстро. Этот эффект более выражен для NaPSS. Это неудивительно, учитывая больший потенциал взаимодействия, где высокая отрицательная линейная плотность заряда вызывает сильные отталкивающие взаимодействия, усиливающие меж- и внутримолекулярные взаимодействия. Падение коэффициента диффузии для PVP происходит более плавно, т.к. он является незаряженным линейным полимером.
Экстраполяция коэффициента диффузии до нулевой концентрации дает гидродинамические диаметры, приближающиеся к 10 нм для PVP и 10-13 нм для NaPSS, что вполне ожидаемо для их Mw. При концентрациях же 50 мг/мл оба полимера находятся в диапазоне выше их критических концентраций перекрытия - C * (объемная доля, выше которой цепи полимера больше не отделены пространственно друг от друга в растворе). Эта критическая концентрация зависит от молекулярной массы, длины цепи и радиуса вращения полимерной цепи. Только по мере приближения к нижней границе полуразведения рассчитанный гидродинамический размер фактически начинает соответствовать размерам цепей.
Резюме
Два основных фактора влияют на нашу способность измерять размер частиц при высоких концентрациях: многократное светорассеяние и взаимодействие частиц друг с другом. Только измерения, производимые в достаточно разбавленных коллоидах, могут быть использованы для надежной интерпретации размера частиц. Даже в отсутствие многократного светорассеяния, измерения, выполненные в области полуразведения, не всегда характеризуют размер частиц, и поэтому при интерпретации таких результатов необходимо соблюдать большую осторожность. Как указано выше, серийное разбавление может использоваться для определения области, в которой образец достаточно разбавлен для надежного измерения.
Статья в изначальном варианте:


